Unstable Plasma zPinch (zPinch.pre)

Keywords: MHD, ideal plasma instabilities

zPinch

Problem description

The Z-Pinch is an ideal MHD simulation of a cylindrical plasma with a purely axial current and a periodic boundary condition in the axial direction. This problem uses a top-hat current density profile such that

\[\begin{equation} \notag \mathbf{J}=\begin{cases} J_{0}\hat{z} & r\leq r_{p}\\0 & r>r_{p}\end{cases} \end{equation}\]

where \(r_p\) is the current column radius. Thus, the magnetic field is

\[\begin{equation} \notag \mathbf{B}=\begin{cases}-\frac{r}{2}\mu_{0}J_{0}\hat{\theta} & r\leq r_{p}\\-\frac{r_{p}^{2}}{2r}\mu_{0}J_{0}\hat{\theta} & r>r_{p}\end{cases}\quad \end{equation}\]

The MHD force balance condition (\(\mathbf{J}\times\mathbf{B}=\nabla p\)) becomes

\[\begin{equation} \notag \frac{dp}{dr}+\frac{B_{\theta}}{\mu_{0}r}\frac{d}{dr}\left(rB_{\theta}\right)\quad, \end{equation}\]

and, thus, the pressure profile is

\[\begin{equation} \notag p=\begin{cases} \frac{\mu_{0}J_{0}^{2}}{4}\left[\left(1+\alpha\right)r_{p}^{2}-r^{2}\right] & r\leq r_{p}\\ \frac{\mu_{0}J_{0}^{2}}{4}\alpha r_{p}^{2} & r>r_{p}\end{cases} \end{equation}\]

where \(\alpha\) sets the base pressure outside the plasma column.

In general, the plasma column may be unstable to perturbations with a wavenumber (\(\mathbf{k}\)) such that

\[\begin{equation} \notag \mathbf{k}=\frac{m}{r}\hat{\theta}+\frac{2\pi n}{Z}\hat{z} \end{equation}\]

where \(m\) is the azimuthal wavenumber, \(n\) is the axial wavenumber, and \(Z\) is the axial length of the computational domain. This example assumes axisymmetry in the azimuthal direction of the cylindrical column, and thus instabilities with \(m=0\) are modeled. The simulation is initialized with a \(n=1\) perturbation in the magnetic field which leads to instability with the default parameters.

This simulation can be performed with a USimBase license.

Creating the run space

The Unstable Plasma Z-Pinch example is accessed from within USimComposer by the following actions:

  • Select the New from Template menu item in the File menu.
  • In the resulting New from Template dialog, expand USimBase: Basic Physics Capabilities.
  • Select Unstable Plasma Z-Pinch and press the Choose button.
  • In the Choose a name for the new runspace dialog, press the Save button to create a copy of this example in your run area.
  • Press the Save And Process Setup button in the upper right corner of the Editor pane.

The basic example variables are editable in the Editor pane of the Setup window as described below. After any change is made, the Save and Process Setup button must be pressed again before a new run may commence.

Input file features

The key variables of the input file are exposed in the Setup window. These variables allow one to set the following fields:

The following parameters control the physics of the Z-Pinch:

  • AXIAL_LENGTH - The axial length of the cylinder.
  • CURRENT - The axial current in the plasma column (\(I=J_0 \pi r_p^2\)).
  • NUM_MODES - Sets the wavenumber
  • BASE_PRESSURE_RATIO - The ratio of the pressure and density at the wall to the pressure and density in the plasma core (\(\alpha\)).
  • PERTURBATION_AMPLITUDE - The relative amplitude of the perturbed field to the field generated by the axial current.
  • GAS_GAMMA - The ratio of specific heats

The following parameters control the dimensionality, domain size and resolution of the simulation:

  • RADIAL_RESOLUTION - The number of radial grid points.
  • AXIAL_RESOLUTION - The number of axial grid points.

The following parameters the length of the simulation and data output:

  • TEND sets the end time for the simulation.
  • NUMDUMPS sets the number of data dumps during the simulation
  • WRITE_RESTART = False,True tells USim to output data necessary to restart the simulation. If this parameter is set to False then the Restart at Dump Number functionality in the Standard tab under Runtime Options in the Run window will not be available.

The following parameters control the USim solvers used to evolve the Z-Pinch:

  • TIME_ORDER = first,second,third,fourth sets the order of accuracy for the time-integration.
  • DIFFUSIVE = False,True sets whether to use diffusive (but robust!) spatial integration schemes.
  • DEBUG = False,True sets whether to output data for debugging a run. Warning: this will output A LOT of information!

Running the simulation

After performing the above actions, continue as follows:

  • Proceed to the Run window as instructed by pressing the Run icon in the workflow panel.
  • To run the simulation, click on the Run button in the upper right corner of the Logs and Output Files pane.

You will also see the engine log output in the Logs and Output Files pane. The run has completed when you see the output, “Engine completed successfully.”

Visualizing the results

After performing the above actions, continue as follows:

  • Proceed to the Visualize window as instructed by pressing the Visualize icon in the workflow panel.
  • Press the Open button to begin visualizing. Select a Data View of Field Analysis.
  • Select fluids/density from the Field dropdown.
  • Click the check box for Log Scale Color Table to view the density using a logarithmic scale.
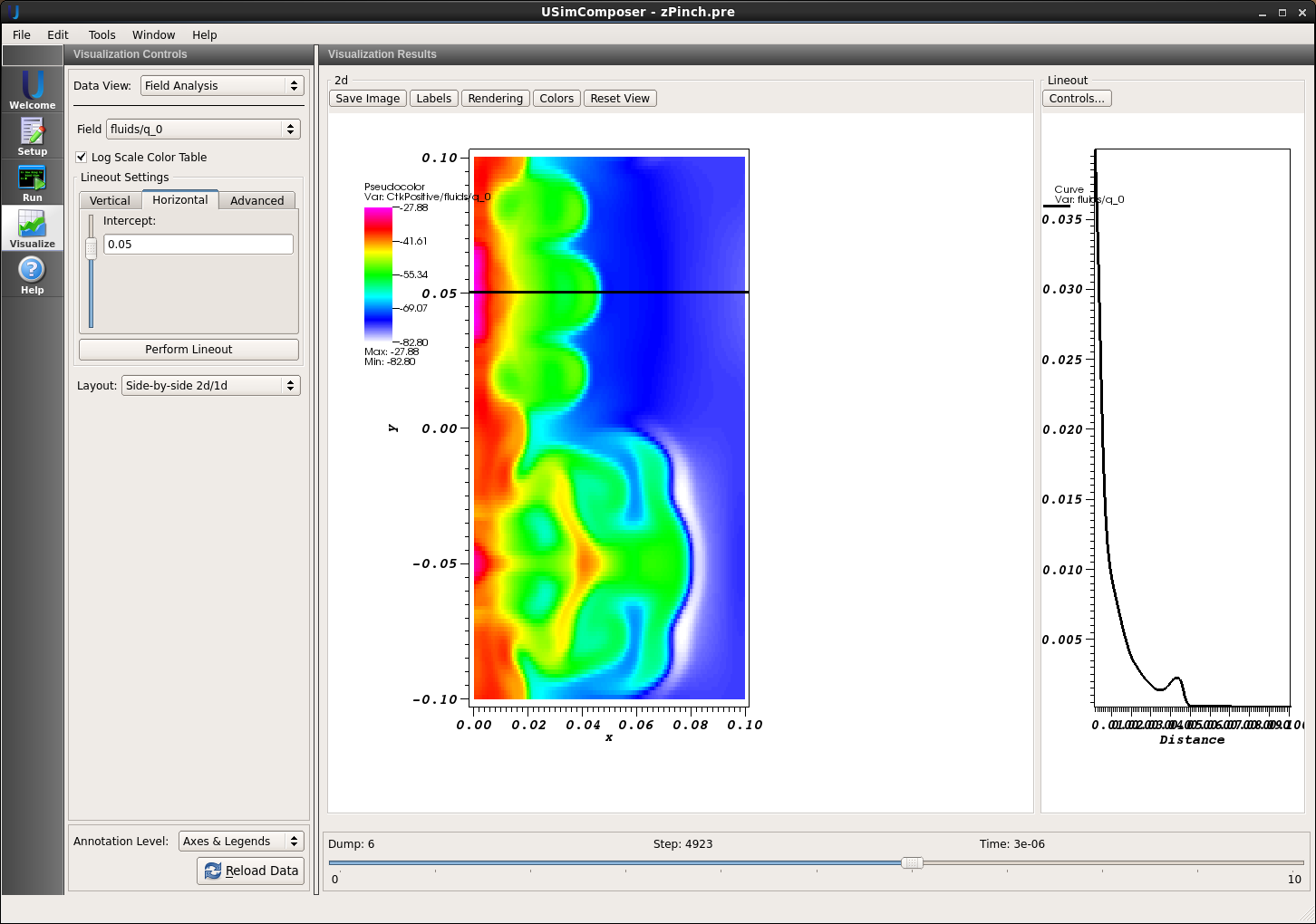
  • Drag the slider at the bottom of the Visualization Results pane to see results for the different simulation data dumps, as shown in Fig. 81.
  • Add a corresponding line plot by adjusting settings in the Lineout Settings pane and pressing the Perform Lineout button to draw.

The plot in Fig. 81 was made with the calewhite color scale at time \(3\times10^{-6}\) seconds. Here the instability is in the nonlinear phase, and the plasma density has ruptured out of the initial plasma column.

Visualization Window

Figure 81: Visualization of the mass density in the Unstable Plasma Z-Pinch example

Further experiments

  • Run the computation into the deep nonlinear stage at current resolution, then run it again with decreased or enhanced resolution. Note there is no dissipation in the ideal MHD system so differing results are expected when dynamics are on the grid-scale length.